SunPathTime
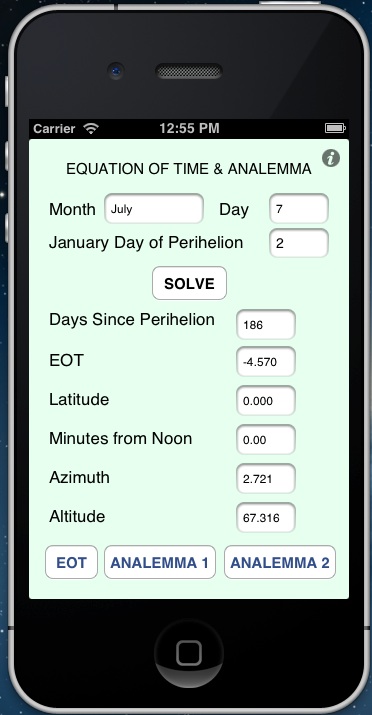
SunPathTime app is a utility app for the calculation of the Equation of Time and the solar Analemma. To use the app simply put in the date and click SOLVE; also put in the day of Perihelion if it‘s different than shown. The pertinent calculated data is shown on the main screen and is also portrayed graphically on the respective screens.
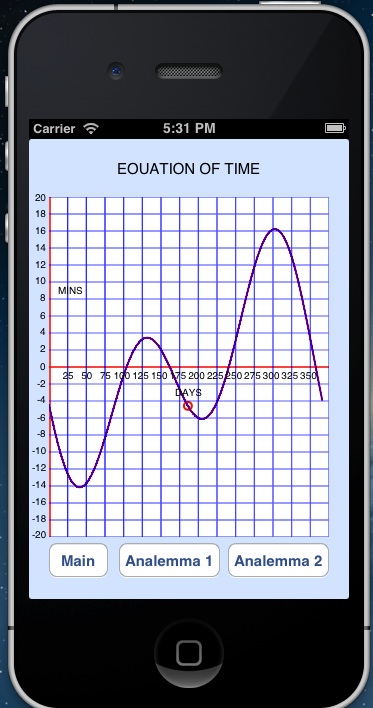
The Equation of Time gives the time difference between apparent solar time and mean solar time. Apparent solar time is reckoned with regard to the actual Sun‘s position. For example apparent noon is when the Sun is directly overhead. This is generally not at 12:00 noon according to the clock, which is that reckoned by a fictitious Sun which travels in its orbit at constant speed. The apparent reckoning takes account of the true Earth orbit around the Sun, which is an ellipse, and the inclination of the Earth‘s axis to the orbital plane. This difference, The Equation of Time, is the same for every observer on Earth. The Equation of Time is given as minutes fast (+) or slow (-) of the Sun with respect to clock time as a function of the day of the year. Sun fast means it is west of the meridian. The two effects of the apparent sun‘s motion, obliquity of the orbit and inclination of the axis, are each approximated by a sine wave of different periods and are additive. Consequently The Equation of Time appears as a distorted sine wave. The reference for the year‘s variation is the point of closest approach of the Earth to the Sun, the perihelion. This date varies from year to year: 1/2/13, 1/4/14, 1/4/15, 1/2/16, 1/4/17, 1/3/18, 1/3/19, 1/5/20.
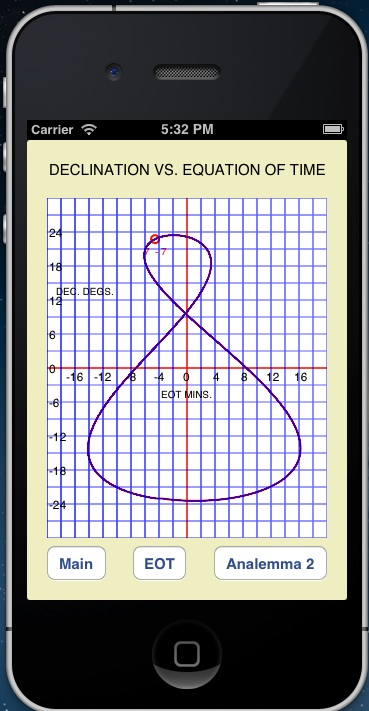
The solar Analemma is the path that the sun traces in the sky when observed at the same mean solar time of day (clock time) over the course of a year. It is a bottom heavy figure of eight pattern that is often portrayed on a world globe. The Sun‘s path in the sky is a combination of two motions. One is the East/West motion due to The Equation of Time and the other is the North/South motion due to the tilt of Earth‘s axis. While The Equation of Time is the same for all observers the Analemma depends on the observer‘s latitude as well as the time of day. If the Analemma is plotted at local noon over the year, the figure‘s axis lines up on a line imagined to go from the South pole to the North pole directly overhead (local noon meridian). If plotted for earlier than noon, it lies on a more easterly meridian and for later than noon it lies on a more westerly meridian. The actual Analemma, can be seen by photographing the Sun over the course of the year (at the same time of day). Examples can be found on the internet. The pattern will be tilted East or West for times other than noon but will be symmetrical to its axis. An artifact of a two dimensional plot is that it will only be symmetrical for the noon Analemma. At other times the plot is distorted due to the transformation of 3D to 2D. So it should be borne in mind that the actual Sun figure is not lopsided.
Analemma 1 is a plot of the sun's declination versus the equation of time. Equatorial celestial coordinates are declination and right ascension or hour angle. These are analagous to latitude and longitude for the earth coordinate system. The declination varies between +23.6 degrees and -23.6 degrees, corresponding to the tilt of earth‘s axis.
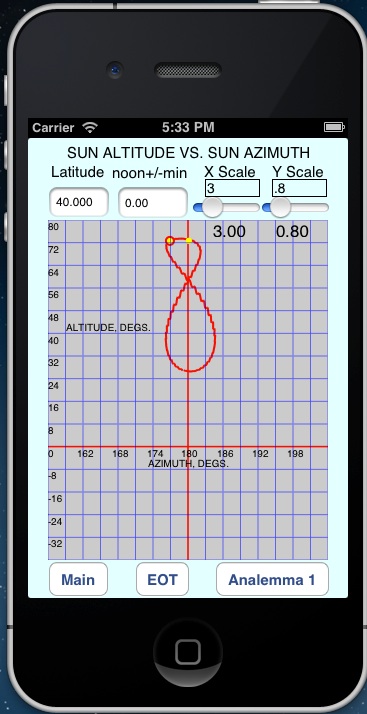
Analemma 2 shows how the sun‘s position varies over the course of a year. The plot is in terms of the local elevation or altitude versus its horizontal position or azimuth. The Analemma can be depicted for different times of day by entering the time in minutes from ST local clock noon for the time zone. An entry of "0" is for noon and the Analemma would be standing up. The two plots would have the same shape at noon if the scaling were equivalent.
The info view provides a handy reference and presents the same information as described here.
Reference: http://en.wikipedia.org/wiki/Equation_of_time http://www.math.nus.edu.sg/aslaksen/projects/tsy.pdf, http://scienceblogs.com/startswithabang/2009/08/26/why-our-analemma-looks-like-a/, http://www.analemma.com
© Copyright Marcus Staloff 2013